- Location
- the details
Everything.
There are things I know that you never can, and vice-versa.
There are things I know that you never can, and vice-versa.
- Pronouns
- He/Him
... you're not making any sense at all to me here. How does any of your last few posts tie into the topic of this thread?
- Location
- the details
Let me ask you a question?
"Is it possible to prove black holes exist without using Relativity?".
I know that the answer to that question is "yes".
Baughn
Healing-type writer
- Location
- Dublin
Nonsense. Analogous objects might exist under different physical laws, but they wouldn't be black holes. The geometry of causality in our universe is what makes them possible in the first place.
- Location
- the details
For every object in the universe, using just classical mechanics, there is a circular orbit radius where the orbital velocity equals the speed of light.
Baughn
Healing-type writer
- Location
- Dublin
In a Galilean universe, the only speed of light which makes the equations of electromagnetics work is infinity. So, not really. That value turns out not to work for other reasons, but all that means is you can't have electromagnetics without relativity. Without electromagnetics you can't have humans.
But let's ignore that. In a Galilean universe there is no upper speed -- relativity is precisely what you get when you require the universe to have a speed limit. Hence, even if your photon-analogues have mass and therefore can travel at finite (and varying!) speed, that's got no bearing on whether or not you can climb out of a black hole. If there is no upper speed then you can, and therefore it isn't black.
There's a third solution, where all four dimensions are space-like. In that one you can reach infinite speed using finite energy, so it doesn't have black holes either.
- Location
- the details
I must wonder, have you ever tried to solve a system where you had more variables than equations?
- Pronouns
- He/Him
Again, how does this tie into anything this thread is about?
- Location
- the details
- Pronouns
- He/Him
That's literally not an answer.
- Location
- the details
It is an answer. It's just not the one you wanted.
- Pronouns
- He/Him
... are you interested, at all, in having a conversation here? Because, look, dropping elementary math truisms off in here -- whose relevance to the actual physical concepts involved in FTL is non-existent -- as if they were deep insights got old real fast, and isn't advancing us anywhere.
- Location
- the details
Perhaps I should step away from this thread. Which I will do from here on out.
We Just Write
Blatantly Plural
- Location
- New England
- Pronouns
- Plural
More seriously, a while back I played around with a Lorentz transformation to figure out how a system analogous to a Warp Drive would behave based on the velocity of the ship prior to going to warp. I came to the following conclusions:
1: If the ship is (roughly) stationary relative to the destination prior to going to warp, it behaves like most space opera. Roughly speaking the observed travel time aboard the ship will match the observed travel time at the destination.
2: If the ship is moving towards the destination prior to warp, the observed travel time aboard will be decreased, but the observed travel time at the destination will be increased.
3: If the ship is moving away from the destination prior to going to warp, observed travel time aboard the ship will increase, but observed travel time at the destination will decrease. If your realspace velocity away from the destination is greater than the inverse of your warp 'velocity', then the observed travel time at your destination will actually be negative and you'll probably wind up in a branch timeline.
1: If the ship is (roughly) stationary relative to the destination prior to going to warp, it behaves like most space opera. Roughly speaking the observed travel time aboard the ship will match the observed travel time at the destination.
2: If the ship is moving towards the destination prior to warp, the observed travel time aboard will be decreased, but the observed travel time at the destination will be increased.
3: If the ship is moving away from the destination prior to going to warp, observed travel time aboard the ship will increase, but observed travel time at the destination will decrease. If your realspace velocity away from the destination is greater than the inverse of your warp 'velocity', then the observed travel time at your destination will actually be negative and you'll probably wind up in a branch timeline.
- Location
- Within hearing range
It sounds like you make the frame of reference of the ship before the jump privileged here. That contradicts the fundamental assertion of relativity that all frames of reference that can be constructed through Lorentz transformations are equally valid.
And from that you get that every "FTL" so space-like separation between points (like the start and end point of a journey) has a frame of reference where it has a negative time component, or a positive one for that matter.
Enh, that isn't quite true. There is a symmetry-breaking privileged frame here -- it's whatever frame the warp drive "starts up" in.
If you imagine that we have a warp drive that boosts you to 5c... well that's a Lorentz boost greater than infinity so lol, but we'll ignore that for now. Anyway, 5c in which frame? Presumably in the frame where you started the device.
The rest basically follows from there. The Lorentz-invariant truth is that the 'angle' (which is actually ill-defined because FTL but again ignoring that for the moment) between the 'stationary' worldline and the 'warp-speed' worldline is equivalent to 5c of boost, and that relative measurement will be the same in all frames -- but there's no rule that says that any of the other results have to be invariant, and in fact if they were relativity would be much less interesting.
Guderian2nd
Your (Future)Emperor
So I've been thinking about this, from the perspective of the person traveling.
In most discussions of FTL(ie. most sci-fi), the stages of an FTL device generally take the form of the following:
1) An FTL device starts out in some initial time-like trajectory in an inertial frame(ie. stationary) - frame S.
2) The FTL device instantaneously switches to some space-like trajectory. Let's call the frame of reference of the FTL device from it's own perspective while it's trajectory is space-like frame F.
3) After some amount of time t_s(> 0) passes in frame S and t_f(>0) in frame F, where t_s does not necessarily have to equal t_f, the FTL device switches back to a time-like trajectory in frame S, from which it's worldline will seem to be space-like - ie. FTL.
I think step 2 is important here, because we can derive some interesting results from it; how does the rest of the universe look like from the FTL spaceship? How much time passes for our FTL spaceship? What is the experience of FTL like for our FTL spaceship? Most discussions of FTL focus on the perspective of frame S, usually to derive the usual time-travel worldlines; but since that's a topic already done to death, I'd like to focus on frame F(if it can even be called a frame) for now.
Let's limit ourselves to a 1+1 spacetime with c=1 for the purposes of simplification.
The one immediate result that we get is that in order to admit frame F as an actual frame from which we can apply Lorentz boosts to, our spacetime cannot be a real vector space. Instead, it must be complex; this seems pretty trivial to demonstrate, since the boost matrix for 1-velocity v is:
And γ(v) is a complex number whenever v > 1.
So, now that spacetime is a complex vector space, suppose that from frame S, starting from (0,0) our FTL spacecraft had a linear trajectory to (x_dest, t_dest) where x_dest/t_dest > 1. What would be the 2-position vector from our FTL spacecraft's perspective(from which we can deduce how the spacecraft will perceive it's own travel time and travel direction)?
Applying the Lorentz Boost:
So far all the equations themselves are nothing different from standard Lorentz boosts. The interesting part happens when we put in FTL numbers.
This actually means that for real-valued FTL velocities, the elapsed proper time for our FTL spacecraft will be imaginary.
For example, if (t_dest, x_dest) = (1,2) - so the FTL velocity of our spacecraft is 2 - then if our FTL craft traveled a distance of 2 in 1 second(from frame S) and then returned to frame S, the time elapsed in the spacecraft itself would be -i seconds - ie. an imaginary amount of time.
This is of course, pretty obviously silly. What does an imaginary amount of time even mean? Since the amount of time elapsed is purely[/I] imaginary, does this mean that our spacecraft didn't experience any travel time at all?
So for the purposes of describing Sci-Fi FTL machines, where clearly a real-amount of proper time is experienced by our space craft, we need to put a constraint; the proper time elapsed for any FTL spacecraft must be a real number. This means that the FTL velocity of our spacecraft must be a complex number; but since we're talking about FTL velocities, it would seem to pose less of a problem for us. Of course, imaginary distances are just as silly as imaginary time in that it is difficult to interpret their semantic, physical meaning, but let's put that aside for now.
This means that if an FTL spacecraft wants to make a journey to a destination with real-numbered time coordinates(technically speaking, since our destination will have complex spacial coordinates we don't actually need to assume this; in essence, it's impossible to travel to a real-numbered spacetime coordinate without "changing" our complex FTL velocity mid-way while still maintaining a real amount of elapsed proper time for our FTL space craft. But let's assume this for now to see what the equations end up looking like) in frame S without changing it's FTL course(ie. constant velocity), it's complex number FTL velocity v must satisfy the following equation:
You get the gist of what I'm trying to do. Gotta go for now, will probably come back later to actually get a relationship between a and b for FTL complex velocity v.
EDIT: hurrdurr mixed up x and t, god damn, hold on while I fix it...
EDIT2: Fixed.
In most discussions of FTL(ie. most sci-fi), the stages of an FTL device generally take the form of the following:
1) An FTL device starts out in some initial time-like trajectory in an inertial frame(ie. stationary) - frame S.
2) The FTL device instantaneously switches to some space-like trajectory. Let's call the frame of reference of the FTL device from it's own perspective while it's trajectory is space-like frame F.
3) After some amount of time t_s(> 0) passes in frame S and t_f(>0) in frame F, where t_s does not necessarily have to equal t_f, the FTL device switches back to a time-like trajectory in frame S, from which it's worldline will seem to be space-like - ie. FTL.
I think step 2 is important here, because we can derive some interesting results from it; how does the rest of the universe look like from the FTL spaceship? How much time passes for our FTL spaceship? What is the experience of FTL like for our FTL spaceship? Most discussions of FTL focus on the perspective of frame S, usually to derive the usual time-travel worldlines; but since that's a topic already done to death, I'd like to focus on frame F(if it can even be called a frame) for now.
Let's limit ourselves to a 1+1 spacetime with c=1 for the purposes of simplification.
The one immediate result that we get is that in order to admit frame F as an actual frame from which we can apply Lorentz boosts to, our spacetime cannot be a real vector space. Instead, it must be complex; this seems pretty trivial to demonstrate, since the boost matrix for 1-velocity v is:
Boost Matrix:
\[
\gamma (v) = {\sqrt{1-v^2}}^{-1}\\
\textbf{B}(v) = \begin{bmatrix} \gamma & -\gamma v \\ -\gamma v & \gamma \end{bmatrix}
\]
And γ(v) is a complex number whenever v > 1.
So, now that spacetime is a complex vector space, suppose that from frame S, starting from (0,0) our FTL spacecraft had a linear trajectory to (x_dest, t_dest) where x_dest/t_dest > 1. What would be the 2-position vector from our FTL spacecraft's perspective(from which we can deduce how the spacecraft will perceive it's own travel time and travel direction)?
Applying the Lorentz Boost:
Elapsed Proper Time for FTL Spacecraft:
\[
\vec{x_{S}} = \begin{pmatrix} t_{dest} \\ x_{dest} \end{pmatrix} : \text{2-position vector} \\
v = x_{dest}/t_{dest} \\
\vec{x_{F}} = \textbf{B}(v)\vec{x_{S}} \\
= \begin{bmatrix} \gamma & -\gamma v \\ -\gamma v& \gamma \end{bmatrix} \cdot \begin{pmatrix} t_{dest} \\ x_{dest} \end{pmatrix} \\
= \begin{pmatrix} \gamma t_{dest} - \gamma v x_{dest} \\ -\gamma v t_{dest} + \gamma x_{dest} \end{pmatrix} \\
= \begin{pmatrix} \gamma (1 - v^2) t_{dest} \\ 0 \end{pmatrix} \\
\]
This actually means that for real-valued FTL velocities, the elapsed proper time for our FTL spacecraft will be imaginary.
For example, if (t_dest, x_dest) = (1,2) - so the FTL velocity of our spacecraft is 2 - then if our FTL craft traveled a distance of 2 in 1 second(from frame S) and then returned to frame S, the time elapsed in the spacecraft itself would be -i seconds - ie. an imaginary amount of time.
This is of course, pretty obviously silly. What does an imaginary amount of time even mean? Since the amount of time elapsed is purely[/I] imaginary, does this mean that our spacecraft didn't experience any travel time at all?
So for the purposes of describing Sci-Fi FTL machines, where clearly a real-amount of proper time is experienced by our space craft, we need to put a constraint; the proper time elapsed for any FTL spacecraft must be a real number. This means that the FTL velocity of our spacecraft must be a complex number; but since we're talking about FTL velocities, it would seem to pose less of a problem for us. Of course, imaginary distances are just as silly as imaginary time in that it is difficult to interpret their semantic, physical meaning, but let's put that aside for now.
This means that if an FTL spacecraft wants to make a journey to a destination with real-numbered time coordinates(technically speaking, since our destination will have complex spacial coordinates we don't actually need to assume this; in essence, it's impossible to travel to a real-numbered spacetime coordinate without "changing" our complex FTL velocity mid-way while still maintaining a real amount of elapsed proper time for our FTL space craft. But let's assume this for now to see what the equations end up looking like) in frame S without changing it's FTL course(ie. constant velocity), it's complex number FTL velocity v must satisfy the following equation:
FTL velocity constraints:
\[
v = a+bi : (a, b \in \textbf{R}) \\
\gamma (1-v^2) = r \in \textbf{R}
\]
You get the gist of what I'm trying to do. Gotta go for now, will probably come back later to actually get a relationship between a and b for FTL complex velocity v.
EDIT: hurrdurr mixed up x and t, god damn, hold on while I fix it...
EDIT2: Fixed.
Last edited:
Has anyone ever considered that the "speed of light" is a really misleading name? I mean, yes that is the speed at which light travels, but its getting cause and effect backwards. Light travels at the speed that it does because that is the maximum speed that anything can travel.
I think we should call it the "speed of information"
You don't need any fancy math to justify why there should be a maximum speed at which information can propagate. There can only be four possible cases:
I think we should call it the "speed of information"
You don't need any fancy math to justify why there should be a maximum speed at which information can propagate. There can only be four possible cases:
- Information has no speed and does not propagate. There is only void
- Information has no speed, all information is available everywhere. Nothing could exist because everything would be affected by an infinite amount of other stuff.
- Information has variable speed. The information about the rate of change in information speed is itself information.
- Information has some fixed speed.
Guderian2nd
Your (Future)Emperor
We already know from Quantum Mechanics(well, classical probability too) that information can technically be instantaneous - that is to say, we can know about the quantum state of some object at event (t,x) before our own clock says it's t+x. Which is a no brainer; even classically, if I have a pair of shoes, put both shoes into different boxes(without me knowing which one is in which), send one of the boxes to Mars, and then open the box left on Earth to observe that it's a left shoe, then I'll instantaneously know that the shoe on mars is a right shoe, even though Mars is 3 light minutes away - ie. I instantaneously acquire information about an object 3 light minutes away. Information is ultimately something in our minds, not something that materially exists.
So unfortunately no, imo, "speed of information" is misleading. "Speed that is invariant" probably makes more sense.
Last edited:
Baughn
Healing-type writer
- Location
- Dublin
To counterpoint: The speed of light is what it is because that's the apparent speed of a null geodesic -- a zero-length four-dimensional path -- as seen from a three-dimensional perspective.
You could also call that the speed of causality, but really it's a fact about geometry. Our universe is four-dimensional and Lorentzian; all interactions are local, including electromagnetic ones; but they're local in the true, four-dimensional geometry. No time passes for photons, because they don't really move at all... from that perspective.
The speed of light is the conversion factor between space and time. They're both dimensions; we just happen to use different units, just like "foot" and "meter". Except in this case it's "second" and "light-second".
- Location
- Within hearing range
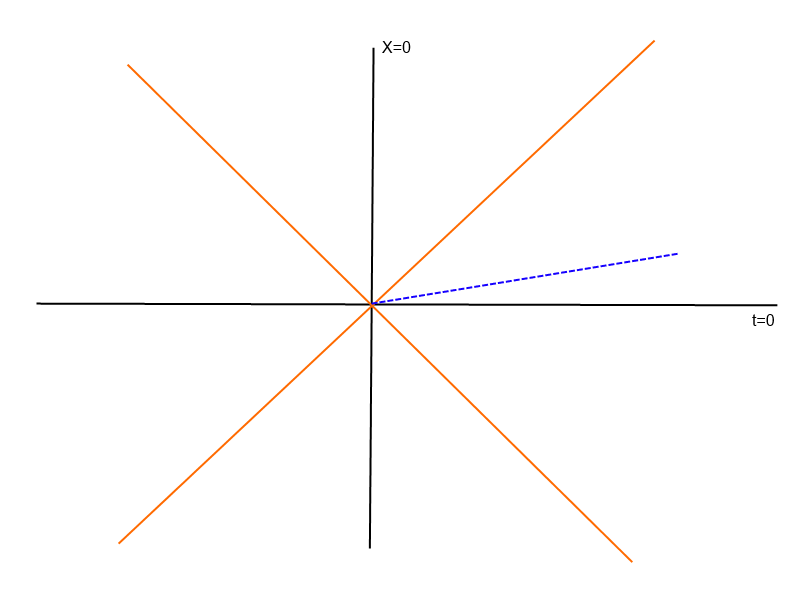
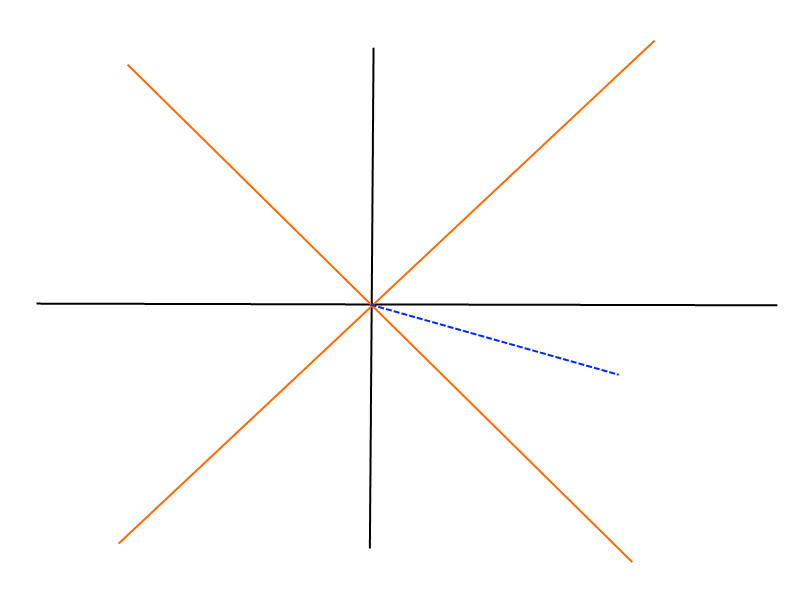
No that's not correct as far as I can tell. If by "angle" you man the euclidean angle between linear worldlines those are not Lorentz-invariant by definition. What is invariant is the dt^2-|dx|^2 which is positive for time-like separations, zero for light-like and negative for space-like. Those cathegories stay fixed between Lorentz trafos but within them anything goes. You define a kind of pseudo-angle that does stay constant I think but that's kind of pointless.
Let's put it in pictures because that's really easy here.
Here I've eyeballed a worldline that covers five times as much distance as light in the same time, so the end coordinate of this FTL trip in this system is (cT,5*cT). Applying a lorentz boost of half the speed of light to the right yields T_new = sqrt(1-0.5^2)*(T-0.5*5T) = ca. -1.3T (and X_new = 3.9cT) so from the perspective of someone travelling to the right at half the speed of light in our initial system it's:
And I see no reason why the first frame of reference should be privileged in any way. The second one is just as valid. It doesn't yet contain a strict causality violation (in the everyday sense of the term) since no cause preceeds it's effect unambigously - but it's trivial to construct such a case by just doing anothe FTL jump at 5c now in the new system back home.
Ah. Well, in that case you have a major conceptual error I want to address first, before I get to the rest of the post.
"All frames of reference are equally valid" means that, no matter what frame of reference you're in, you must observe the same events, and all Lorentz scalars must have their same value. It does not mean that different frames of reference can observe different things. They certainly do, but only when they are observing things that, well, aren't Lorentz-invariant.
The time by your personal clock, of anything other than yourself, is not a Lorentz scalar, and neither is the order of events according to your reference frame. However, the actual events themselves are invariant -- all the relativity "paradoxes", like the pole vaulter and the barn door and so on, work out so that everyone still agrees that, for the same example, the pole vaulter makes it all the way through the barn without colliding with the walls, and so on. Similarly, the proper time according to any observer -- their own personal age -- is also a Lorentz invariant; that age may be less or greater in your time frame, a hundred years might speed by in an instant for you, but if you sit down and do the math you must calculate the same age for whatever you're looking at as is experienced by that same object.
To give a concrete example -- even in our day to day life, there's no objective speed. A car that is driving by me at 60 mph, might also be falling behind the car in the next lane at -5mph. However, the difference between the car's speed and my speed, or the car's speed and that of the car in the next lane, are things we will all agree on (so long as we aren't near the speed of light, anyway!) -- those are "Galilean scalars," as it were, numbers that are invariant under Galilean velocity transforms. It's the difference between saying "I and you both see the same thing," and "You see thing A, and I see you seeing thing A, even though I see thing B."
Crucially, by the way, the existence of an actual closed timelike curve is an 'event' that must be invariant. Whether or not FTL is possible, there cannot be a way to make a worldline intersect itself purely by application of Lorentz boosts, even FTL Lorentz boosts; doing so would itself contradict Lorentz invariance.
Travel time aboard the ship is the proper time of the ship. Observed travel time of the ship at the destination is also a form of proper time -- depending on the details of the destination frame it will not agree with anyone else's observation of the ship's travel time, but everyone will agree that the destination observed X amount of time while waiting for the ship to arrive.
As such, nothing in @I just write's post directly contradicts Lorentz invariance. I haven't actually checked his work -- though the results sound somewhat similar to what I remember doing when I did the same thing a while ago -- but at the very least there isn't a major obvious flaw.
Now, on the topic of angles...
Nope, I mean the hyperbolic angle between worldlines.
Let's talk about rapidity for a second here, because that's actually the real fundamental quantity; speed is just the bit that's easy for us as humans to measure. We motivate this as follows:
First, consider the Lorentz boost transformation itself. If we boost in some direction by some scaled velocity β, then (t,x) in the original coordinate frame transforms as
LaTeX:
\[
\begin{align} \Lambda_\beta \vec{x} &\equiv \begin{pmatrix}\gamma & -\gamma\beta\\ -\gamma\beta & \gamma \end{pmatrix} \begin{pmatrix}ct\\x\end{pmatrix}\\ \gamma&=\frac{1}{\sqrt{1-\beta^2}}\end{align}
\]
But it then immediately follows from the definitions of gamma and beta that γ2-(γβ)2=1. Then we can define, for some w we shall call the rapidity, that tanh(w)=β, or
LaTeX:
\[
\begin{align}\sinh w &= \gamma\beta\\ \cosh w &= \gamma \\ \Lambda_w \vec{x} &= \begin{pmatrix}\cosh w & -\sinh w\\-\sinh w & \cosh w\end{pmatrix}\end{align}
\]
This matrix should look rather familiar -- it's almost the form of a rotation matrix. In fact, it is precisely the form of a rotation matrix with imaginary argument; equivalently, a rotation in hyperbolic space -- which is precisely the geometry of Minkowski spacetime. Thus we see that the intuition of a speed as a sort of angle through space-time is an entirely rigorous notion. In fact, in many ways it is more rigorous, more physically valid -- because after all, the arctanh of v=c, β=1 is infinity. So duh you can't go faster than light, because you can't boost (rotate) by an angle "more than infinity"; and on top of that, duh the speed of light is constant in all reference frames, because 'infinity' can be defined as "the point that is equidistant to all points on the number line".
(For bonus points, it also makes the velocity-addition formula much less mysterious:
LaTeX:
\[
\begin{align}\beta^{\prime}&=\frac{\beta_{0}+\beta}{1+\beta_{0}\beta}\\
\to\tanh w^{\prime}&=\frac{\tanh w_{0}+\tanh w}{1+\tanh w_{0}\tanh w}\\
&=\tanh(w_0 + w)
\end{align}
\]
Now, intuitively we would expect that, as with Euclidean rotations, hyperbolic angles are themselves invariant under hyperbolic rotation. In fact, arguably I've already proved that with the velocity-addition rewrite just above; but let's double-check this. Just like in Euclidean geometry, we can write the inner product of two vectors as a function of the (hyperbolic) cosine of the angle between them:
LaTeX:
\[
\begin{align} \vec{r_{1}}=\left(ct_{1},x_{1}\right)&=r_{1}\left(\cosh w_{1},\sinh w_{1}\right)\\\vec{r_{2}}=\left(ct_{2},x_{2}\right)&=r_{2}\left(\cosh w_{2},\sinh w_{2}\right)\\\vec{r_{1}}\cdot\vec{r_{2}}&=r_{1}r_{2}\left(\cosh w_{1}\cosh w_{2}-\sinh w_{1}\sinh w_{2}\right)\\&=r_{1}r_{2}\cosh\left(w_{1}-w_{2}\right)\end{align}
\]
But it's trivial to show that the inner product is invariant under a Lorentz boost:
LaTeX:
\[
\Lambda \vec{r_1}\cdot\Lambda \vec{r_2} = (\Lambda \vec{r_1})^T(\Lambda \vec{r_2}) = \vec{r_1}^T \Lambda^T \Lambda \vec{r_2}=\vec{r_1}^T \vec{r_2}=\vec{r_1}\cdot\vec{r_2}
\]
and so the hyperbolic angle between two four-vectors must be as well.
Now, when we try to apply this to FTL, weird shit happens; unlike a circle, the most general hyperbola has two 'types,' one opening to +/- x and one opening to +/- y, and we'll have to cross from one to the other in order to make the concept of a single, well defined "angle" meaningful -- i.e. maintain our inner product rule above and keep all our parameters real. In turn, this implies that you can't measure the angle between a spacelike and a timelike four-vector and expect it to come out real -- it will have to be complex, that can't be avoided with any consistent definition of sinh/cosh/tanh. However, aside from being yet another indictment of the plausibility of straightforward, locally-traveling-faster-than-light FTL, once you do make that concession it's not clear to me that any of the above should stop being true; that complex 'angle,' rather unphysical though it might be, should still be conserved under a Lorentz boost.
In other words, if it is true that "In my current reference frame, my warp drive will instantaneously place me in a reference frame moving 5c in the opposite direction," then all other observes must agree that "In his reference frame, his warp drive will instantaneously place him in a reference frame moving 5c in the opposite direction," even if they themselves observe him moving at some different speed, or even going backward in time.
Last edited:
We Just Write
Blatantly Plural
- Location
- New England
- Pronouns
- Plural
Something I forgot to mention: when I was doing my Lorentz transformation, I didn't model the warp trajectory by just tilting the timelike axis for the ship outside the light cone. Instead, I determined the proper angle for the ship's realspace velocity, then added the warp trajectory as a third line sliding sideways relative to the timelike axis. This is to model how GR-compliant warp drive metrics don't actually accelerate the ship past c, but instead move the chunk of spacetime the ship occupies without imparting any acceleration forces whatsoever.